suyc's blog

哎，什么时候才能把英语学好啊🙇‍~

two-kmp-methods

Posted on In

kmp简单来说就是，描述了一个前缀的最长公共前后缀。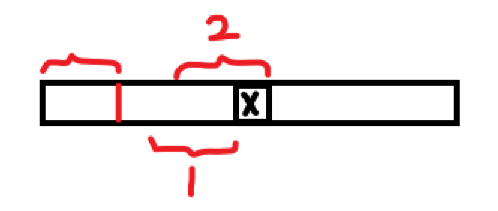

关于kmp的算法，有很多人也写过了，我主要记录以下关于这个前缀是否包含当前节点的问题。也就是对图中X点来说的1和2两种情况。

情况1：不包含当前节点

我觉得这种情况也是最容易理解的了。例子：

i 0 1 2 3 4 5 6 7 8 9
s a b c a b c a b d #
next 0 0 0 0 1 2 3 4 5 0

对于上述串的s[4]来说，b的前缀是abca，公共前后缀是1。
值得关注的点是s[8]，它的前缀是abcabcab，公共的前后缀为abcab，当匹配的时候，如果遇到s[8]和目标串的某位不相同，则可跳转到s[5]，s[5]!=s[8]就是kmp的精髓。
另外一点是有时候s[9]是额外增加的一个#，它并不属于串s，因为有些时候需要对s做个统计，看一下它的公共前后缀，则可使用多余的这一位。

代码如下：

1
2
3
4
5
6
7
8
vector<int> getNext(const string &pattern) {
    vector<int> next(pattern.size() + 1);
    for (int i = 2, j = 0; i <= pattern.size(); ++i) {
        while (j && pattern[i - 1] != pattern[j]) j = next[j];
        if (pattern[i - 1] == pattern[j]) next[i] = ++j;
    }
    return next;
}

很容易理解，i代表当前节点，i-1和j比较即代表了前缀是否相等，并不包含当前节点。

情况2：包含当前节点

例子：

i 0 1 2 3 4 5 6 7 8
s a b c a b c a b d
next -1 -1 -1 0 1 2 3 4 -1

代码如下：

1
2
3
4
5
6
7
8
9
10
vector<int> getNext(const string &pattern) {
    vector<int> next(pattern.size(), -1);
    for (int i = 1, j = -1; i < pattern.size(); ++i) {
        while (j != -1 && pattern[j + 1] != pattern[i]) {
            j = next[j];
        }
        if (pattern[j + 1] == pattern[i]) next[i] = ++j;
    }
    return next;
}

全部初始化为-1，j+1和i相比较，i代表当前节点，所以这个结果next中的i是和当前节点相关的。
next[i] + 1即可代表一个包含i位的前缀的最长公共前后缀。这个可以直接统计某个位置的前缀是否存在公共前后缀，不存在则为-1，对s来说，它不存在最长的公共前后缀，所以s[8] = -1。

比较

其实，情况2往后错一位即和情况1吻合。所以要具体问题具体分析，看题目中更适合哪种情况。

i 0 1 2 3 4 5 6 7 8 9
s a b c a b c a b d #
next1 0 0 0 0 1 2 3 4 5 0
next2 -1 -1 -1 0 1 2 3 4 -1 -
next2’ - -1 -1 -1 0 1 2 3 4 -1
Related Posts